Option Pricing Calculator
The option calculator on the home page allows you to define the parameters that you need to calculate and generate theoretical prices and option risk values for European style call and put options. Together with these values you'll notice dynamically drawn payoff graphs that illustrate your theoretical profit and loss as well as your payoff after the option contract has expired.
Black and Scholes
The mathematical formula behind these calculations is called the Black and Scholes option model (1973).
The idea behind pricing an option contract comes down to two things: the expected payoff of the option at expiration and the probability of the option expiring in the money. The formual is described as...
Call Option =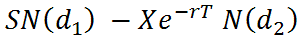 
Put Option =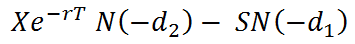 
Where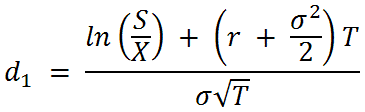 
And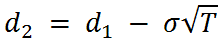 
S = Stock Price
X = Exercise Price
r = Risk Free Interest Rate
T = Time to Expiration (Years)
N(x) = The Cumulative Normal Distribution Function
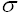= Standard Deviation
Source Code
You can request the spreadsheet that this site was based on with the full VBA used here:
Implied Volatility
It is impossible to reverse the Black Scholes formula and solve for volatility.
So instead, I use a high/low routine and iterate through a range of numbers to generate the implied volatility.
I use the market price as the output for Black and Scholes and use this method to solve for the volatility input that would generate the price that equals the market price.
Here is a snippet from my VBA code:
High = 5
Low = 0
Do While (High - Low) > 0.0001
If OTW_BlackScholes("c", "p", UnderlyingPrice, ExercisePrice, Time, Interest, (High + Low) / 2, Dividend) > Target Then
High = (High + Low) / 2
Else: Low = (High + Low) / 2
End If
Loop
OTW_IV = (High + Low) / 2
Where "(High + Low) / 2" is normally the volatility input.
I use a maximum of 500% for the upper limit.
Volatility Day Count
When estimating volatility, it is necessary to annualise the input used. Originally it was standard to use a 365 day calendar year, however, these days many option traders are opting to use a 256 trading day calendar as it is stated that volatility can only occur while the markets are open.
Option-Price, however, uses a 365 calendar year.
Dividends
Dividends are inserted as an annual effective yield, rather than discrete values.
Options on Futures
Pricing options on futures is slightly different to stock options. The difference comes down to the forward price.
Stocks use the interest rate component to determine the expected cost of holding the underlying until the expiration date. With a futures contract, the future contracts price IS the forward price, so there is no need to use the interest rate for that purpose.
There is, however, a need for the interest rate component in order to discount the premium of the option.
To get around this with standard Black and Scholes, just enter the interest rate as normal and then use the same value for the Dividend Yield.
This way, the forward price will come back to the spot (futures) price (interest - dividend yield) but the interest rate will still be used as the rate for discounting the option premium.
Profit and Loss Graphs
Notice also that the P&L line seen in the Payoff Graphs displays the actual profit or loss, not the theoretical value of the position. This is why the line always crosses the x axis at the underlying price point.
If you want to see the theoretical value changing across a price grid, then please use the Simulation feature at the bottom of the home page.
Contact Me
If anything is not clear about this site, please don't hesitate to contact me.